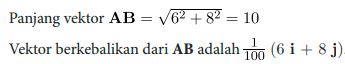Rangkuman Materi Vektor dan Operasinya MTK SMA Kelas 10
Marikuliah.com - Halo sobat pintar! Pada artikel ini kami akan memberikan rangkuman materi MTK SMA Kelas 10 Vektor dan Operasinya kurikulum merdeka.
Materi ini dipelajari oleh siswa kelas 10 pada mata pelajaran MTK kurikulum merdeka atau kurikulum 2021.
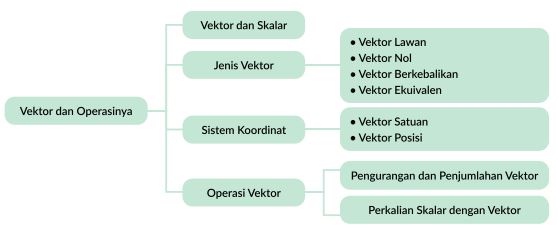
Sebelum kamu menyelami lebih lanjut rangkuman materi Vektor dan Operasinya, ada baiknya kamu terlebih dahulu memperhatikan peta konsep berikut ini:
Rangkuman Materi Vektor dan Operasinya
Apa itu vektor?
Apa itu skalar?
- Besaran skalar hanya mempunyai besar atau nilai, tidak mempunyai arah.
- Contoh besaran skalar adalah massa melon 2,00 kg.
- Semua bilangan real merupakan skalar, dapat bernilai nol atau positif atau negatif.
Notasi vektor
Notasi vektor adalah sebagai berikut:
1. Panjang dan Arah Vektor
2. Vektor Negatif atau Vektor Lawan
- Vektor A menyatakan perpindahan Andi yang pertama.
- Vektor -A menyatakan perpindahan Andi yang kedua.
- Vektor A dan -A sama panjang tetapi berlawanan arah.
- -A adalah vektor lawan dari A.
Vektor negatif atau vektor lawan adalah vektor dengan besar sama, tetapi arah berlawanan dengan suatu vektor.
Vektor Nol
Vektor nol adalah vektor dengan panjang nol dan tidak punya arah tertentu atau vektor dengan titik pangkal dan ujung yang sama. Vektor nol dinyatakan dengan titik secara grafis.
3. Vektor Ekuivalen (Vektor yang Sama)
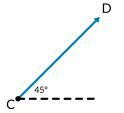
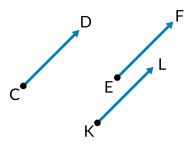
Jika ada vektor lain dengan panjang 3 cm dan sudut 45°, maka dikatakan vektor tersebut ekuivalen dengan vektor CD.
CD = EF = KL
Vektor CD ekuivalen dengan vektor EF dan vektor KL.
Vektor dan Sistem Koordinat
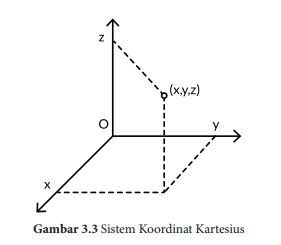
Lokasi suatu titik dapat dinyatakan dalam sistem koordinat Kartesius. Pada sistem koordinat dua dimensi, lokasi titik dinyatakan dalam pasangan terurut (x, y) dan pada sistem koordinat tiga dimensi, lokasi titik dinyatakan dalam (x, y, z).
1. Vektor Berdimensi Dua pada Sistem Koordinat
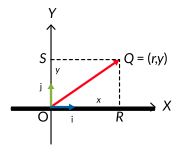
- Koordinat titik O adalah (0, 0) dan Q adalah (x, y). Vektor satuan diperlukan untuk menunjukkan bagaimana mencapai titik Q dari titik O.
- i adalah vektor satuan dalam arah-x (horizontal) dan j adalah vektor satuan dalam arah-y (vertikal). Vektor satuan mempunyai besar 1 satuan. Arah horizontal negatif dinyatakan dengan -i dan arah vertikal negatif dinyatakan dengan -j.
- Vektor OQ dinyatakan sebagai berikut.
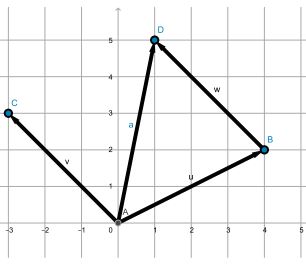
2. Vektor-Vektor Ekuivalen pada Sistem Koordinat Kartesius
Vektor u dan v ekuivalen, dinyatakan dengan 4 i + 3 j, walau keduanya mempunyai koordinat titik pangkal dan koordinat titik ujung yang berbeda. Komponen horizontal dan komponen vertikal adalah 4 dan 3.3. Vektor Berdimensi Tiga pada Sistem Koordinat Kartesius
Vektor dengan tiga komponen, disebut sebagai vektor berdimensi tiga.
i adalah vektor satuan dalam arah-x (horizontal), j adalah vektor satuan dalam arah-y (vertikal) dan k adalah vektor satuan, yang tegak lurus terhadap bidang xy. Arah horizontal negatif dinyatakan dengan -i, arah vertikal negatif dinyatakan dengan -j dan arah negatif dalam z dinyatakan dengan -z.
4. Vektor Kolom dan Vektor Baris
Vektor yang dituliskan dalam bentuk kolom adalah vektor kolom. Vektor yang dituliskan dalam bentuk baris adalah vektor baris. Komponen-komponen vektor kolom dituliskan sebagai berikut.
5. Vektor Posisi
Vektor posisi adalah vektor yang berpangkal di titik O yang merupakan pusat koordinat dan berujung di suatu titik dalam sistem koordinat.
6. Vektor Berkebalikan
Vektor AB = 6 i + 8 j
Operasi Vektor
1. Penjumlahan Vektor
Hasil penjumlahan vektor disebut sebagai resultan vektor.
- Penjumlahan Dua Vektor dengan Metode Segitiga
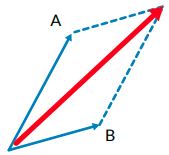
- Penjumlahan Dua Vektor dengan Metode Jajar Genjang
- Penjumlahan dengan Metode Poligon
- Penjumlahan Vektor secara Komponen
2. Pengurangan Vektor
Hasil pengurangan vektor disebut sebagai resultan vektor.
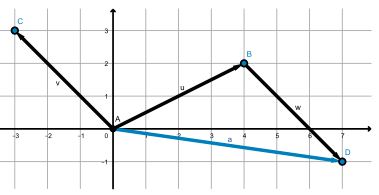
AB – AC = AB + (–AC) = (4 2) + (3 –3) = (7 –1)
- Vektor Nol
Vektor nol adalah vektor dengan panjang nol dan tidak punya arah tertentu atau vektor dengan titik pangkal dan ujung yang sama.