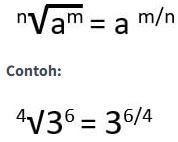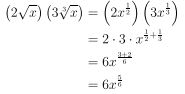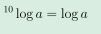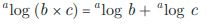Rangkuman Materi Eksponen dan Logaritma

Marikuliah.com - Halo sobat pintar! Pada artikel ini kami akan membagikan rangkuman materi MTK kelas 10 bab 1 Eksponen dan Logaritma.

Materi ini dipelajari oleh siswa kelas 10 pada mata pelajaran MTK kurikulum merdeka atau kurikulum 2021.

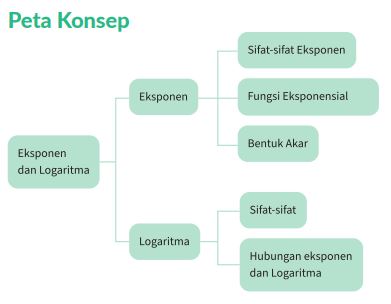
Sebelum kamu menyelami lebih lanjut rangkuman materi Eksponen dan Logaritma, ada baiknya kamu terlebih dahulu memperhatikan peta konsep berikut ini:

Rangkuman Materi Eksponen dan Logaritma

Definisi Eksponen

Perkalian berulang adalah perkalian yang dilakukan secara berulang dengan faktor yang sama.

Contoh:

• 2×2×2×2×2×2 ditulis dengan 2⁶
• 5×5×5×5×5×5×5×5 ditulis dengan 5⁸
• 15×15×15×15 ditulis dengan 15⁴
• 7×7×7×7×7×7×7×7×7×7 ditulis dengan 7¹⁰
• a×a×a×a×a×a×a ditulis dengan a⁷

Sifat-sifat eksponen

1. Pangkat Penjumlahan

a^m . aⁿ = a^{m + n}    (perkalian basis sama (a) maka pangkatnya bisa ditambah)

Contoh: 4² . 4³ = 4^{2 + 3} = 4⁵

 

2. Pangkat Pengurangan

a^m : aⁿ = a^{m – n}    (pembagian basis yang sama, maka pangkatnya bisa dikurang)

Contoh: 4⁵ : 4³ = 4^{5 – 3} = 4²

 

3. Pangkat Perkalian

(a^m)ⁿ = a^{m x n}    (jika bilangan berpangkat dipangkatkan lagi, maka pangkatnya harus dikali)

Contoh: (4²)³ = 4^{2 x 3} = 4⁶

 

4. Perkalian Bilangan yang Dipangkatkan

(a . b)^m = a^m . b^m    (perkalian bilangan yang dipangkatkan, maka masing-masing bilangan tersebut bisa dipangkatkan juga)

Contoh: (3. 5)² = 3². 5²

5. Perpangkatan pada Bilangan Pecahan

6. Pangkat Negatif

7. Pangkat Pecahan

8. Pangkat nol

a⁰ = 1

(syaratnya a bukan nol)

Contoh: 12⁰ = 1

Fungsi Eksponen

Sebuah fungsi eksponen dinyatakan dengan:

f(x) = n × a^x

di mana a adalah bilangan pokok, a > 0, a ≠ 1, n adalah bilangan real tak nol dan x adalah sebarang bilangan real.

Contoh: f(x) = 3^x

1. Pertumbuhan Eksponen 

Pertumbuhan berbanding lurus dengan besarnya nilai kuantitasnya.

Contoh soal:

Untuk mengamati pertumbuhan suatu bakteri pada inangnya, seorang peneliti mengambil potongan inang yang sudah terinfeksi bakteri tersebut dan mengamatinya selama 5 jam pertama. Pada inang tersebut, terdapat 30 bakteri. Setelah diamati, bakteri tersebut membelah menjadi dua setiap 30 menit.

1. Modelkan fungsi pertumbuhan bakteri pada setiap fase.
2. Gambarkan grafik pertumbuhan bakteri tersebut.
3. Pada jam ke-5 berapa banyak bakteri baru yang tumbuh?

Penyelesaian:

1. Pada awal pengamatan, bakteri yang diamati berjumlah 30 sehingga untuk 30 menit berikutnya dapat digambarkan pertumbuhan bakterinya sebagai berikut Misalkan x adalah fase pertumbuhan bakteri setiap 30 menit, maka

Fase (30 menit)	0	1	2	3	4	5
Banyak bakteri	30	60	120	240	480	960

Untuk x = 0, banyak bakteri = 30

Untuk x = 1, banyak bakteri = 60

Untuk x = 2, banyak bakteri = 120 = 2².30;

Untuk x = 3, banyak bakteri = 240 = 2³.30;

Untuk x = 4, banyak bakteri = 480 = 2⁴.30;

Pertumbuhan bakteri dapat dimodelkan dengan fungsi eksponen.

f(x) = 30.(2^x) 

2. Grafik:

Gunakan aplikasi GeoGebra untuk membantu kalian menggambarkan grafik tersebut. Kunjungi www.geogebra.org.

3. Jam ke-5 terjadi pada fase ke-10 (ingat kembali pembelahan terjadi setiap 30 menit), sehingga:

 
Jadi banyak bakteri yang tumbuh pada jam ke-5 atau fase ke-10 adalah 30.720 bakteri.

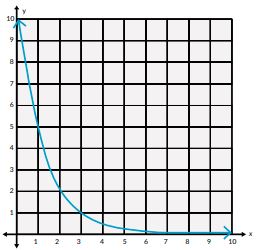
2. Peluruhan Eksponen

Definisi: menggambarkan penurunan secara konsisten pada periode waktu tertentu

f(x ) = n^x × a 

dengan 0 < a < 1, n bilangan real tak nol, x adalah sebarang bilangan real.

Grafik:

Contoh soal:

Obat penahan rasa sakit disuntikkan kepada pasien yang mengalami luka berat akibat kecelakaan. Dosis obat yang disuntikkan adalah 50 mikrogram. Satu jam setelah penyuntikan, setengah dosis tersebut akan luruh dan dikeluarkan dari dalam tubuh. Proses tersebut akan terus berulang setiap jam.

1. Berapa banyak dosis obat yang masih tertinggal di dalam tubuh pasien setelah 1 jam, 2 jam, dan 3 jam?
2. Bagaimana model matematika yang dapat menyatakan peluruhan dosis obat tersebut? 

Penyelesaian:

1. Dosis awal = 50 mikrogram Misalkan dosis pada x waktu dilambangkan dengan f(x), maka:

2. Berdasarkan bagian a, fungsi eksponen yang dapat menyatakan peluruhan dosis obat tersebut dari dalam tubuh pasien pada jam tertentu adalah:

dengan x adalah waktu yang dibutuhkan obat tersebut untuk meluruh sebanyak setengah dosis dari dosis sebelumnya.

Bentuk Akar

1. Hubungan Bilangan Pangkat dan Akar

Hubungan bilangan bentuk akar dan bilangan berpangkat adalah bentuk akar merupakan kebalikan dari bilangan berpangkat.

Contoh soal:

Sederhanakanlah bentuk berikut:

untuk x > 0

Penyelesaian:

2. Merasionalkan Bentuk Akar

Untuk merasionalkan bentuk akar, maka yang dapat dilakukan adalah dengan mengalikannya dengan bentuk akar sekawannya.

Logaritma

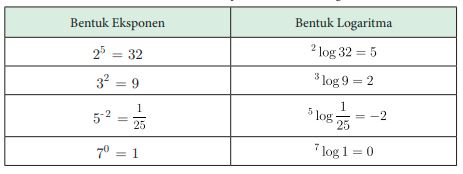
1. Definisi Logaritma

Logaritma adalah inversi atau kebalikan dari eksponen. 

Logaritma yang memiliki basis 10 disebut dengan logaritma umum dan dituliskan sebagai berikut:

2. Sifat-sifat logaritma

Contoh soal logaritma:

Buktikan sifat logaritma berikut:

Penyelesaian:

Rangkuman Materi Eksponen dan Logaritma

• Download rangkuman eksponen dan logaritma .pdf
• Download materi eksponen dan logaritma lengkap

Nah itulah tadi adalah pembahasan tentang materi MTK SMA kelas 10 Bab 1 tentang Eksponen dan Logaritma. Semoga artiekl rangkuman materi Eksponen dan Logaritma ini dapat membantu kamu ya.

Berbagi :