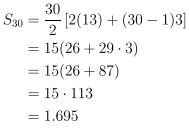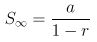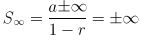Rangkuman Materi Barisan dan Deret MTK SMA Kelas 10 Kurikulum Merdeka
Marikuliah.com - Halo sobat pintar! Pada artikel ini kami akan memberikan rangkuman materi MTK SMA Kelas 10 barisan dan deret kurikulum merdeka.
Materi ini dipelajari oleh siswa kelas 10 pada mata pelajaran MTK kurikulum merdeka atau kurikulum 2021.
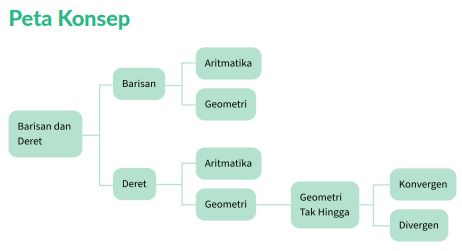
Sebelum kamu menyelami lebih lanjut rangkuman materi Barisan dan Deret, ada baiknya kamu terlebih dahulu memperhatikan peta konsep berikut ini:
Rangkuman Materi Barisan dan Deret
Rangkuman Barisan
Barisan merupakan daftar angka yang mengurut dari kiri ke kanan. Setiap pola urutan memiliki karakteristik tertentu. Barisan dibagi menjadi dua yakni barisan aritmatika dan barisan geometri.
1. Barisan Aritmatika
Contoh:
*polanya selalu ditambah dengan dua.
Untuk mencari beda dapat dilakukan dengan cara mengurangkan dua suku yang berurutan
b = U2 – U1
b = U3 – U2
b = U4 – U3 dan seterusnya.
Rumus:
Un = a + (n - 1) b
Keterangan:
- Un = suku ke-n
- a = suku pertama
- n = nomor suku
- b = beda
Contoh soal:
Diketahui suatu barisan aritmetika, suku ke-3 = 9, suku ke-6 = 18. Tentukan rumus suku ke-n!
Penyelesaian:
Jadi, rumus suku ke-n dari barisan tersebut adalah Un = 3n.
2. Barisan Geometri
- Barisan geometri adalah suatu barisan dengan rasio antara dua suku berurutan selalu tetap atau konstan.
- Rasio pada barisan geometri dilambangkan dengan r.
Rumus:
Jadi, rasio pada barisan geometri dapat dinyatakan dengan:
Un = a.rn-1
- Un = suku ke-n
- a = suku pertama
- n = nomor suku
- r = rasio
Contoh soal:
Suku pertama dari suatu barisan geometri adalah 4 dan suku ke-4 adalah 108. Tentukan rasio dari barisan tersebut.
Rangkuman Deret Bilangan
Deret bilangan adalah jumlah suku-suku penyusun barisan bilangan. Dertet bilangan dibagi menjadi 3 yakni deret aritmatika, deret geometri dan deret geometri tak hingga.
1. Deret Aritmetika
Rumus deret aritmatika:
- Sn = jumlah deret sebanyak n suku pertama
- a = suku pertama
- b = beda
- n = banyaknya suku
Contoh soal:
Suku pertama atau a = 13b = 3n = 30
2. Deret Geometri
Deret geometri adalah jumlah dari barisan bilangan yang suku-sukunya membentuk barisan geometri.
Rumus deret geometri:
Keterangan:- Sn = jumlah deret sebanyak n suku pertama
- a = suku pertama
- r = rasio
- n = banyaknya suku
Hasil produksi sebuah perusahaan sepeda pada tahun 2020 meningkat setiap bulannya dan membentuk barisan geometri. Produksi pada bulan Januari sebanyak 120 unit. Pada bulan April, hasil produksi mencapai 3.240 unit. Berapakah total hasil produksi sepeda hingga bulan Mei?
Penyelesaian:
Hasil produksi Januari: U1 = a = 120Hasil produksi April: U1 = 3.240
Total hasil produksi hingga bulan Mei: S5Sebelum menentukan S5 , harus dicari ratio (r) terlebih dahulu.
3. Deret Geometri Tak Hingga
- Deret geometri tak hingga adalah penjumlahan suku-suku pada baris geometri yang jumlahnya tak hingga. Ada dua konvergen dan divergen.
- Divergen tak memiliki limit.
- Konvergen (memusat) memungkinkan masih memiliki limit.
Deret geometri tak hingga divergen dengan r < -1 atau r > 1:
Contoh soal:Tentukan jumlah deret tak hingga dari 81 + 27 + 9 + 3 + …..
Penyelesaian:
Deret tak hingga di atas merupakan deret tak hingga konvergen, karena r = 1/3 masuk dalam rentang -1 < r < 1, maka jumlah deret tak hingga adalah:
Download Rangkuman Materi Barisan dan Deret MTK SMA Kelas 10 Kurikulum Merdeka
Nah demikianlah adalah pembahasan dari marikuliah.com tentang rangkuman materi barisan dan deret MTK SMA Kelas 10 pada kurikulum 2021 atau kurukulum meredeka. Semoga rangkuman materi barisan dan deret ini dapat membantu kamu ya. Jangan lupa share ke kawan-kawan kamu juga ya.






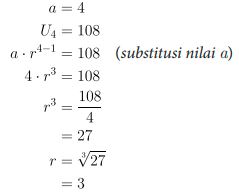
.JPG)